【330592】第21章达标检测卷3
第二十一章 一次函数
测试题
一、选择题(每小题3分,共24分)
1.某人要在规定的时间内加工100个零件,则工作效率 与时间
与时间 之间的关系中,下列说法正确的是(
).
之间的关系中,下列说法正确的是(
).
(A)数100和 ,
, 都是变量
都是变量
(B)数100和 都是常量
都是常量
(C) 和
和 是变量
是变量
(D)数100和 都是常量
都是常量
2. 汽车离开甲站10千米后,以60千米/时的速度匀速前进了 小时,则汽车离开甲站所走的路程
小时,则汽车离开甲站所走的路程 (千米)与时间
(千米)与时间 (小时)之间的关系式是(
).
(小时)之间的关系式是(
).
(A)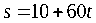 (B)
(B) (C)
(C) (D)
(D)
3.(课本39页习题1变形)如图,若输入 的值为-5,则输出的结果(
).
的值为-5,则输出的结果(
).
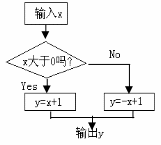
(A)―6 (B)―5 (C)5 (D)6
4.下列图表列出了一项实验的统计数据,表示将皮球从高 处落下时,弹跳高度
处落下时,弹跳高度 与下落高度
与下落高度 的关系:
的关系:
-

50
80
100
150
25
40
50
75
则能反映这种关系的式子是( ).
(A) (B)
(B)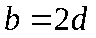 (C)
(C) (D)
(D)
5.下列函数中,自变量 不能为1的是(
).
不能为1的是(
).
(A) (B)
(B) (C)
(C) (D)
(D)
6.下列图形中的曲线不表示 是
是 的函数的是(
)
的函数的是(
)

(B)![]()
7 .
甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示。根据图中提供的信息,有下列说法:
.
甲乙两同学从A地出发,骑自行车在同一条路上行驶到B地,他们离出发地的距离s(千米)和行驶时间t(时)之间的函数关系的图象,如图所示。根据图中提供的信息,有下列说法:
他们都行驶了18千米。
甲车停留了0.5小时。
乙比甲晚出发了0.5小时。
相遇后甲的速度小于乙的速度。
甲、乙两人同时到达目的地。
其中符合图象描述的说法有( )
(A)2个 (B)3个 (C)4个 (D)5个
8.如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.

① ② ③ ④
 运动员推出去的铅球(铅球的高度与时间的关系)
运动员推出去的铅球(铅球的高度与时间的关系)
 静止的小车从光滑的斜面滑下(小车的速度与时间的关系)
静止的小车从光滑的斜面滑下(小车的速度与时间的关系)
 一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系)
一个弹簧由不挂重物到所挂重物的质量逐渐增加(弹簧的长度与所挂重物的质量的关系)
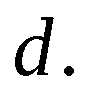 小明从A地到B地后,停留一段时间,然后按原速度原路返回(小明离A地的距离与时间的关系)
小明从A地到B地后,停留一段时间,然后按原速度原路返回(小明离A地的距离与时间的关系)
正确的顺序是( )
(A) (B)
(B) (C)
(C) (D)
(D)
二、填空题(每小题3分,共24分)
9.已知等式 ,则
,则 关于
关于 的函数关系式为________________.
的函数关系式为________________.
10.
市场上一种豆子每千克售2元,即单价是2元/千克,豆子总的售价 (元)与所售豆子的数量
(元)与所售豆子的数量 kg之间的关系为_______,当售出豆子5kg时,豆子总售价为______元;当售出豆子10kg时,豆子总售价为______元.
kg之间的关系为_______,当售出豆子5kg时,豆子总售价为______元;当售出豆子10kg时,豆子总售价为______元.
11.函数是表达现实世界中数量之间变化规律的一种数学模型,它的三种数学表示方法分别为_________、_________、_________.
12.函数 中自变量
中自变量 的取值范围是______________.
的取值范围是______________.
13.导弹飞行高度 (米)与飞行时间
(米)与飞行时间 (秒)之间存在着的数量关系为
(秒)之间存在着的数量关系为 ,当
,当 时,
时, ____________.
____________.
14.如图,表示一辆汽车行驶的速度和时间的图象,你能用语言描述汽车的行驶情况吗?________________________________.

15.用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律搭下去,搭 个三角形需要
个三角形需要 支火柴棒,那么
支火柴棒,那么 与
与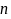 的关系可以用式子表示为
(
的关系可以用式子表示为
( 为正整数).
为正整数).

16.假定甲、乙两人在一次赛跑中,路程S与时间t的关系如图所示,看图填空:
(1)这是一次_______赛跑.(2)甲、乙两人中先到达终点的是_________.
(3)乙在这次赛跑中的平均速度是_________ /
/ .
.

三、问答题(共40分)
17.(10分)长方形的周长为20cm,它的长为 cm,宽为
cm,宽为 cm.
cm.
(1)上述的哪些是常量?哪些是变量?
(2)写出 与
与 满足的关系式;
满足的关系式;
(3)试求宽 的值分别为2,3.5时,相应的长
的值分别为2,3.5时,相应的长 是多少?
是多少?
(4)宽为多少时,长为8cm?
18.(10分)如图所示,三角形的底边长为8cm,高为 cm.
cm.
(1)写出三角形的面积 与高
与高 之间的函数关系式;
之间的函数关系式;
(2)用表格表示高从5cm变到10cm时(每次增加1cm) 的对应值;
的对应值;
(3)当 每次增加1cm时,
每次增加1cm时, 如何变化?说说你的理由.
如何变化?说说你的理由.
19.(10分)如图,表示甲骑电动自行车和乙驾驶汽车的均行驶90km的过程中,行驶的路程 与经过的时间
与经过的时间 之间的函数关系,请根据图象填空:
之间的函数关系,请根据图象填空:
_________出发的早,早了________小时,_____________先到达,先到_________小时,电动自行车的速度为__________km/h,汽车的速度为__________km/h.

20.(10分)填表并观察下列两个函数的变化情况:
-

1
2
3
4
5
…


(1)在同一个直角坐标系中画出这两个函数的图象,比较它们有什么不同(说出一条不同点即可)?
(2)预测哪一个函数值先到达100.
四、试一试(12分)
21.(12分)小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).
(1)图象表示了哪两个变量的关系?
(2)10时和13时,他分别离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)11时到12时他行驶了多少千米?
(5)他可能在哪段时间内休息,并吃午餐?
(6)他由离家最远的地方返回时的平均速度是多少?

参考答案:
1.C;
2.A;
3.D;
4.C;
5.B;
6.C;
7.C;
8.D;
9. ;
;
10. ,10,20;
,10,20;
11.图像法,表达式法,表格法;
12. ;
;
13. 4443.75;
14.答案不唯一,略;
15. ;
;
16.(1)100 ,(2)甲
,(3)8;
,(2)甲
,(3)8;
17.(1)常量是20,变量是 ,
, .
.
(2)因为 ,所以
,所以 .
.
(3)当 时,
时, ;当
;当 时,
时, ;
;
(4)当 时,
时, .
.
18.(1) (
( );
);
(2)
-
 (cm)
(cm)5
6
7
8
9
10
 (cm2)
(cm2)20
24
28
32
36
40
(3)当 每增加1cm,
每增加1cm, 相应地增加4cm2.
相应地增加4cm2.
19.甲(或电动自行车),2,乙(或汽车),2,18,90;
20.填表如下:
-

1
2
3
4
5
…

12
14
16
18
20
…

5
10
15
20
25
…
(1)不同点有:① 图象不经过原点,
图象不经过原点, 图象经过原点;②当
图象经过原点;②当 时,
时,
 图象在
图象在 图象上方,当
图象上方,当 时,
时, 图象在
图象在 图象下方;③随着
图象下方;③随着 增大,
增大, 的值比
的值比 的值增大的快等.
的值增大的快等.
(2) 的函数值先到达100.
的函数值先到达100.
21.(1)时间与距离;
(2)10时和13时,分别离家10千米和30千米;
(3)到达离家最远的时间是12时,离家30千米;
(4)11时到12时,他行驶了13千米;
(5)他可能在12时到13时间休息,吃午餐;
(6)共用了2时,因此平均速度为15千米/时.
- 1【330924】综合平移的坐标表示
- 2【330923】专题练习2:用计算器求平均数
- 3【330921】轴对称的坐标表示
- 4【330922】专题练习1:用计算器求平均数
- 5【330920】中心对称和中心对称图形
- 6【330919】直角三角形全等的判定
- 7【330918】直角三角巷的性质和判定(Ⅰ)
- 8【330917】正方形
- 9【330916】正比例函数的图象和性质
- 10【330915】长丰县2018-2019学年度第二学期期末考试八年级数学参考答案
- 11【330914】用待定系数法确定一次函数表达式
- 12【330913】一次函数知识点总结
- 13【330911】一次函数与一次方程的联系
- 14【330912】一次函数知识点归纳
- 15【330908】新人教版初中数学八年级下册同步练习试题及答案_第20章 数据的分析(22页)
- 16【330910】一次函数的图象和性质
- 17【330909】一次函数
- 18【330907】新人教版八年级数学下第18章《平行四边形》单元试卷
- 19【330906】新人教版八年级数学下第16章《二次根式》单元试卷
- 20【330904】湘教版八年级数学下《第5章数据的频数分布》单元试卷含答案
- 【330905】湘教版八年级数学下册全册综合测试题
- 【330903】湘教版八年级数学下《第3章图形与坐标》单元试卷含答案
- 【330901】湘教版八年级数学下《第1章直角三角形》单元试卷含答案
- 【330902】湘教版八年级数学下《第2章四边形》单元试卷含答案
- 【330900】五种类型一次函数解析式的确定
- 【330899】同步练习试题及答案_第19章 一次函数(10页)
- 【330898】同步练习试题及答案_第18章 平行四行形(40页)
- 【330897】同步练习试题及答案_第17章 勾股定理(20页)
- 【330896】同步练习试题及答案_第16章 二次根式(19页)
- 【330894】思想方法专题:直角三角形中的思想方法
- 【330895】特殊平行四边形知识点归纳
- 【330893】思想方法专题:矩形中的折叠问题
- 【330892】思想方法专题:勾股定理中的思想方法
- 【330891】数学培优辅差工作计划3
- 【330890】数学培优辅差工作计划2
- 【330889】数学培优辅差工作计划1
- 【330888】三角形的中位线
- 【330887】人教版数学八年级上同期末达标检测卷2
- 【330886】人教版数学八年级上同期末达标检测卷1
- 【330885】人教版数学八年级上册期中达标测试卷