【330828】平行四边形创新题赏析

平行四边形创新题赏析

平行四边形部分是初中数学的重点内容，在各地中考试卷中都占有一定的分量。随着课程改革的进一步深入，出现了许多构思新、重素质、考能力的创新题型，令人耳目一新；它对培养和考查学生的发散能力和综合能力大有裨益。现例举中考题几例并加以归类浅析，希望对同学们有所启发。

一、补充说理型

例1. 如图1，已知四边形ABCD是平行四边形，∠BCD的平分线CF交边AB于F，∠ADC的平分线DG交边AB于G。

（1）求证：AF＝GB；

（2）请你在已知条件的基础上再添加一个条件，使得△EFG为等腰直角三角形，并说明理由。

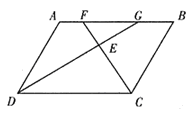
图1

解析：（1）∵四边形ABCD是平行四边形

∴AB∥CD，∴∠AGD＝∠CDG

又∵DG是∠ADC的平分线

∴∠ADG＝∠GDC

∴∠AGD＝∠ADG

∴AD＝AG

同理可得：BF＝BC

在平行四边形ABCD中，AD＝BC

∴AG＝BF

∴AF＝GB

（2）可以添加条件∠ADC＝90°或四边形ABCD是矩形

说理如下：∵四边形ABCD是矩形

∴∠ADC＝∠BCD＝90°

又DG、CF平分∠ADC和∠BCD

∴∠EDC＝∠ECD＝45°

∴∠AGD＝∠BFC＝45°，∠FEG＝90°

即△EFG是等腰直角三角形。

点评：此例把解题的主动性交给学生，让学生添加条件再说理，给学生创造了一个适度的思维空间；富有创意，活而不难，有利于激发学生的信心和探索欲望。

二、判断类比型

例2.

已知任意四边形ABCD，且线段AB、BC、CD、DA、AC、BD的中点分别是E、F、G、H、P、Q。

（1）若四边形ABCD如图2-1，判断下列结论是否正确（正确的在括号里填“√”，错误的在括号里填“×”）。

甲：顺次连接EF、FG、GH、HE一定得到平行四边形；（ ）

乙：顺次连接EQ、QG、GP、PE一定得到平行四边形。（ ）

（2）请选择甲、乙中的一个，证明你对它的判断。

（3）若四边形ABCD如图2-2，请你判断（1）中的两个结论是否成立？

解析：（1）甲的判断是正确的；乙的判断是错误的。

（2）对甲说理如下：

连接EF、FG、GH、HE（如图2-3）

∵E、F分别是AB、BC的中点

∴EF是△ABC的中位线

同理，HG∥AC

∴EF∥HG，EF＝HG

∴四边形EFGH是平行四边形

对乙可举反例说明：如图2-4，在矩形ABCD中，顺次连接EQ、QG、GP、PE得到一条线段，而不是一个平行四边形。

（3）对图2-2，类似于（1）中的结论甲、乙都成立。

点评：此例通过设计问题串，让学生经历判断、归纳，从而建立认识，再作判断；体现了新课程下命题者关注学生思维过程的良苦用心。

三、猜想证明型

例3.

已知：如图3，四边形ABCD是菱形，E是BD延长线上一点，F是DB延长线上一点，且DE＝BF。请你以F为一个端点，和图中已标明字母的某一点连成一条新的线段，猜想并证明它和图中已有的某一条线段相等（只须证明一组线段相等即可）。

图3

（1）连接_____________；

（2）猜想_____________＝_____________；

（3）证明

解析：连接AF，猜想AF＝AE。

证明：连接AC，交BD于O

∵四边形ABCD是菱形，∴AC⊥BD于O，DO＝BO

∵DE＝BF，∴EO＝FO

∴AC垂直平分EF

∴AF＝AE

点评：此例要求学生经历探索—猜想—证明的思维过程，这种螺旋上升的结构符合学生的心理特征和认知规律。让考生在试卷上留下思维的痕迹，能创造性地激活学生的思维。

四、运动探究型

例5.

如图4，已知平行四边形ABCD及四边形外一直线 ，四个顶点A、B、C、D到直线 的距离分别为a、b、c、d。

（1）观察图形，猜想得出a、b、c、d满足怎样的关系式？证明你的结论。

（2）现将 向上平移，你得到的结论还一定成立吗？请分情况写出你的结论。

解析：（1）

证明：连接AC、BD，且AC、BD相交于点O， 为点O到 的距离

图4

∴ 为直角梯形 的中位线

同理：

（2）不一定成立。

分别有以下情况：

直线 过A点时， ；

直线 过A点与B点之间时， ；

直线 过B点时， ；

直线 过B点时与D点之间时， ；

直线 过D点时， ；

直线 过C点与D点之间时， ；

直线 过C点时， ；

直线 过C点上方时， 。

点评：将静态的数学与动态的变化结合起来，给数学以生命，让学生在图形的变化中理解体验变与不变。本题以“平行四边形”、“线”为背景，在“动”中开拓学生视野，拓宽学生的思维空间，在“静”中寻找关系，从而找到解决问题的途径。该题较好地考查了学生观察、分析、判断论证能力和探究创新能力；有利于培养学生严谨的思维习惯和缜密的治学态度。

五、图形设计型

例5.

在△ABC中，借助作图工具可以作出中位线EF，沿着中位线EF一刀剪切后，用得到的△AEF和四边形EBCF可以拼成平行四边形EBCP，剪切线与拼图如图示1，仿上述的方法，按要求完成下列操作设计，并在规定位置画出图示。

图示1

（1）在△ABC中，增加条件_____________，沿着_____________一刀剪切后可以拼成矩形，剪切线与拼图画在图示2的位置；

（2）在△ABC中，增加条件_____________，沿着_____________一刀剪切后可以拼成菱形，剪切线与拼图画在图示3的位置；

（3）在△ABC中，增加条件_____________，沿着_____________一刀剪切后可以拼成正方形，剪切线与拼图画在图示4的位置；

（4）在△ABC（AB≠AC）中，一刀剪切后也可以拼成等腰梯形，首先要确定剪切线，其操作过程（剪切线的作法）是____________________________

然后，沿着剪切线一刀剪切后可以拼成等腰梯形，剪切线与拼图画在图示5的位置。

解：（1）方法一：∠B＝90°，中位线EF，如图示2-1。

方法二：AB＝AC，中线（或高）AD，如图示2-2。

（2）AB＝2BC（或者∠C＝90°，∠A＝30°），中位线EF，如图示3。

（3）方法一：∠B＝90°且AB＝2BC，中位线EF，如图示4-1。

方法二：AB＝AC且∠BAC＝90°，中线（或高）AD，如图示4-2。

（4）方法一：不妨设∠B＞∠C，在BC边上取一点D，作∠GDB＝∠B交AB于G，过AC的中点E作EF∥GD交BC于F，则EF为剪切线，如图示5-1。

方法二：不妨设∠B＞∠C，分别取AB、AC的中点D、E，过D、E作BC的垂线，G、H为垂足，在HC上截取HF＝GB，连接EF，则EF为剪切线，如图示5-2。

方法三：不妨设∠B＞∠C，作高AD，在DC上截取DG＝DB，连接AG，过AC的中点E作EF∥AG交BC于F，则EF为剪切线，如图示5-2。

点评：重视提高动手操作能力和实践能力，是素质教育新课程的切入点。此类题设计新颖，不落俗套，为考生画图操作、类比联想、反思探究提供了自由发挥、自主探究的广阔思维空间；对进一步理解和应用所学知识，发展创新能力、实践能力、操作能力大有裨益；让学生在具体的操作情境中，领悟数学的发展与形成的真谛。

初三中考作业本有这样一道题:如图所示,已知四边形纸片ABCD,现需将该纸片剪拼成一个与它面积相等的平行四边形纸片,如果限定裁剪线有两条,能否做到:____(选填"能"或"不能"),请确定裁剪线的位置,并说明拼接方法:若填"不能",请简要说明理由.

拿到此题,学生们感觉无从下手.仔细分析此题,此题涉及到如何剪,如何拼的问题,因而我作了如下的解题分析.

一.寻找解题思路.

(1)由于四边形内角和为3600,因而可以将四个内角拼成一个周角,可以进行平面镶嵌.

(2)由于拼成的四边形是平行四边形,因而必须注意边长的特殊性,可以取各边的中点.

在找到思路的基础上,我们就可动手裁剪--沿对边的中点剪开,分割成四部分.

二.如何拼凑是本题的难点,关键是不能将剪下的图形弄乱.拼时以其中一块图形不动,抓相等的边拼在一起,以相临两边的中点为旋转中心将其中两块图形转1800,不相临的第三块图形平移到空缺处.

三.如何说明它是平行四边形.

(1)必须说明三点共线.可用两角之和为1800.

(2)必须说明它是平行四边形.可用角的关系证明两组对边平行.

经过以上的分析,裁剪,拼凑,证明,才可完整的完成此题.