【330721】第一章 三角形的证明 周周测9（1.3~1.4）

1. 三角形的证明周周测7

线段的垂直平分线与角的平分线

一、选择题

1．如图1，在△ABC中，AD平分∠CAE，∠B= ，∠CAD= ，则∠ACD等于 （ ）

A． B． C． 　 D．

2．如图2，在△ABD中，AD=4，AB=3，AC平分∠BAD，则 = （ ）

A． B． C． 　 D．不能确定

3．如图3，在△ABC中，∠C= ，AD平分∠BAC，DE⊥AB于E，则下列结论：①AD平分∠CDE；

②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB。其中正确的有 （ ）

A．2个 B．3个 C．4个　 D．1个

4．如图4，AD∥BC，∠D= ，AP平分∠DAB，PB平分∠ABC，点P恰好在CD上，则PD与PC的大小关系是 （ ）

A ．PD>PC B．PD<PC C．PD=PC D．无法判断

。

5、在三角形内部，有一点P到三角形三个顶点的距离相等，则点P一定是 （ ）

A、三角形三条角平分线的交点；B、三角形三条垂直平分线的交点；

C、三角形三条中线的交点；D、三角形三条高的交点。

6、已知△ABC的三边的垂直平分线交点在△ABC的边上，则△ABC的形状为 （ ）

A、锐角三角形；B、直角三角形；C、钝角三角形；D、不能确定

7、如图所示，在△ABC中，∠BAC＝90°，AD⊥BC于D，BE平分∠ABC交AD于E，F在BC上，并且BF＝AB，则下列四个结论：①EF∥AC，②∠EFB＝∠BAD，③AE＝EF，④△ABE≌△FBE，其中正确的结论有 （　 ）

A、①②③④　　　　　B、①③　　　　　C、②④　　　　　D、②③④

7题图 8题图 9题图

8、如图所示，在 中，∠C＝90°， AC＝4㎝，AB＝7㎝，AD平分∠BAC交BC于D，DE⊥AB，则EB的长是 （ 　　）

A、3㎝　　　　B、4㎝　　　　　C、5㎝　　　　D、不能确定

9、随着人们生活水平的不断提高，汽车逐步进入到千家万户，小红的爸爸想在本镇的三条相互交叉的公路（如图所示），建一个加油站，要求它到三条公路的距离相等，这样可供选择的地址有（　　　）处。

A、1　　　B、2　　　　C、3　　　　　　D、4

10、到三角形三条边的距离都相等的点是这个三角形的 （　　 ）

Ａ．三条中线的交点 Ｂ．三条高的交点

Ｃ．三条边的垂直平分线的交点 Ｄ．三条角平分线的交点

二、填空题。

1. 如图，在 中， ， 平分 ， ，那么 点到直线 的距离是　　　　　　cm．

2 ．如图，在Rt△ABC中，∠C=90°，∠A=30°，BD是∠ABC的平分线，若BD=10，则 点到 的距离是

B

3 ．如图，△ABC中，AB=AC，DE是AB的垂直平分线， AB=8，BC=4，∠A=36°，则∠DBC= ，△BDC的周长C_△BDC = ．

4．如图，∠1=50°，∠2=80°，DB=AB，CE=CA，则∠D= ，∠DAE= ．

5．如图，ΔABC的三边AB、BC、CA的长分别是20、30、40、其中三条角平分线将ΔABC分为三个三角形，则S ：S ：S 等于______.

三、解答题

1 ．如图所示，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，求PD的长．

2．已知：E是∠AOB的平分线上一点，EC⊥OA ，ED⊥OB ，垂足分别为C、D．

求证：（1）∠ECD=∠EDC ；（2）OE是CD的垂直平分线．

3．如图，已知在△ABC中，AB=AC，∠BAC=120^o，AC的垂直平分线EF交AC于点E，交BC于点F．求证：BF=2CF．

4．如图所示，∠BAC＝105°，MP和NQ分别垂直平分AB和AC．求∠PAQ的度数．

5、如图所示，在△ABC中，AD是角平分线，DE⊥AB于点E，DF⊥AC于点F，

求证：（1）AE=AF，（2）DA平分∠EDF

6、如图，在△ABC 中，AB=AC，D是BC边上的一点，DE⊥AB，DF⊥AC，垂足

分别为E、F，添加一个条件，使DE= DF， 并说明理由．

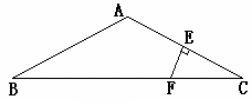
7、如图，已知：AD平分 ，EF垂直平分AD，交BC延长线于F，连结AF。

求 证： 。

答案：

一、1~5 CABCB 6~10 BAADD

二、1.3 2.5 3.36° 12 4.25° 115° 5.2:3:4

三、1.解：如图，过点P作PE⊥OB于E，
∵PC∥OA，
∴∠AOP=∠CPO，
∴∠PCE=∠BOP+∠CPO=∠BOP+∠AOP=∠AOB=30°，
又∵PC=4，

∵AOP=∠BOP，PD⊥OA，
∴PD=PE=2．

2.证明：（1）∵E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，
∴EC=DE，
∴∠ECD=∠EDC；
（2）在Rt△OCE和Rt△ODE中，

∴Rt△OCE≌Rt△ODE（HL），
∴OC=OD，
又∵OE是∠AOB的平分线，
∴OE是CD的垂直平分线．

3.证明：连接AF，
∵AB=AC，∠BAC=120°，

∵AC的垂直平分线EF交AC于点E，交BC于点F，
∴CF=AF（线段垂直平分线上的点到线段两端点的距离相等），
∴∠FAC=∠C=30°（等边对等角），

∴∠BAF=∠BAC-∠FAC=120°-30°=90°，
在Rt△ABF中，∠B=30°，
∴BF=2AF（在直角三角形中，30°角所对的直角边等于斜边的一半），
∴BF=2CF（等量代换）．

4. 解：∵∠BAC=105°，
   ∴∠ABP+∠ACQ=180°-105°=75°，
   ∵MP、NQ分别垂直平分AB和AC，
   ∴PB=PA，QC=QA．
   ∴∠PAB=∠ABP，∠QAC=∠ACQ，
   ∴∠PAB+∠QAC=∠ABP+∠ACQ=75°，
   ∴∠PAQ=105°-75°=30°．

4. 证明：（1）∵AD是角平分线，DE⊥AB于点E，DF⊥AC于点F，
   ∴在△ADE和△ADF中

∴△ADE≌△ADF（AAS），
∴AE=AF．
（2）由（1）知△ADE≌△ADF，
∴∠ADE=∠ADF，
∴DA平分∠EDF．

4. 解：需添加的条件是：BD=CD，或BE=CF．
   添加BD=CD的理由：
   ∵AB=AC，
   ∴∠B=∠C．
   又∵DE⊥AB，DF⊥AC，
   ∴∠BED=∠CFD=90°．
   ∴△BDE≌△CDF（AAS）．
   ∴DE=DF．
   添加BE=CF的理由：
   如图，∵AB=AC，
   ∴∠B=∠C．
   ∵DE⊥AB，DF⊥AC，
   ∴∠BED=∠CFD．
   又∵BE=CF，
   ∴△BDE≌△CDF（ASA）．
   ∴DE=DF．

4. 证明：∵EF垂直平分AD，∴AF=DF，∠ADF=∠DAF，
   ∵∠ADF=∠B+∠BAD，
   ∠DAF=∠CAF+∠CAD，
   又∵AD平分∠BAC，
   ∴∠BAD=∠CAD，
   ∴∠B=∠CAF．